定义

http://people.csail.mit.edu/silvio/Selected%20Scientific%20Papers/Proof%20Systems/The_Knowledge_Complexity_Of_Interactive_Proof_Systems.pdf

零知识协议是一种方法，通过这种方法，一方（证明者）可以向另一方（验证者）证明某事是真实的，除了证实特定声明之外，不会透露任何信息。

在16世纪的文艺复兴时期，意大利有两位数学家为竞争一元三次方程求根公式发现者的桂冠，就采用了零知识证明的方法。当时，数学家塔尔塔里雅和菲奥都宣称自己掌握了这个求根公式，为了证明自己没有说谎，又不把公式的具体内容公布出来(可能在当时数学公式也是一种技术秘密)，他们摆开了擂台：双方各出30个一元三次方程给对方解，谁能全部解出，就说明谁掌握了这个公式。比赛结果显示，塔尔塔里雅解出了菲奥出的全部30个方程，而菲奥一个也解不出。于是人们相信塔尔塔里雅是一元三次方程求根公式的真正发现者，虽然当时除了塔尔塔里雅外，谁也不知道这个公式到底是个什么样子。

零知识证明的应用场景

https://ethereum.org/zh/zero-knowledge-proofs/#use-cases-for-zero-knowledge-proofs

匿名支付
身份保护
认证
可验证计算
减少链上投票中的回路和串通

如何证明交易发起者？
每个用户都有一对公钥和密钥来管理钱包，公钥类似于银行账户的用户名，私钥类似于账户密码，账户地址是根据公钥通过不可逆算法算出来的字符串，公钥和地址都是可以公开的，私钥是需要个人妥善保管的。如果要证明这笔交易的发起方确实是小明，小明的钱包如果将私钥打包在交易中，那全网都知道了小明的私钥，相当于小明的银行卡密码被泄露了，那小明的资产就极其不安全。所以私钥不能泄露，多少比特币用户早年因为私钥丢了，结果当初不值钱的比特币现在已经是一笔巨款，简直是拍断大腿。
因此，接下来的问题是怎么在不泄露私钥的情况下证明这笔交易确实是有小明自己发起的，然后让网络上形成共识让这笔交易入链，交易完成后，小明才能喝到咖啡，咖啡店才能收到钱。这就是个很典型的零知识证明问题。

零知识证明的原理

证明

证明 x = 3 是 x^3^+x+5 = 35 的解

转换为计算函数

1
2
3

def qeval(x):
    y = x**3
    return x + y + 5

拍平（flatten）

将函数转为两种形式的语句
x = y
和
x = y op z
其中 op 可以是 +、* （- 和 / ？）
这种表达式可以看作是电路中的逻辑门，每一条语句称为一个 约束

sym_1 = x * x
y = sym_1 * x
sym_2 = y + x
~out = sym_2 + 5

R1CS

将拍平的表达式转为 R1CS（rank-1 constraint system）电路。
R1CS 是一组长度为3的向量(a, b, c)，其中解向量 s满足
s·a * s·b - s·c = 0

解向量 s 一般称为 witness

向量构造方式就是拍平后的表达式的变量的系数。
首先将所有变量排列， ~one 表示常量 1
'~one', 'x', '~out', 'sym_1', 'y', 'sym_2'

第一行

sym_1 = x * x

=>

1 * x + 1 * x - 1 * sym_1 = 0

所以

1
2
3

a = [0, 1, 0, 0, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 1, 0, 0]

同理，剩下3行的向量分别为

y = sym_1 * x
=>
a = [0, 0, 0, 1, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 0, 1, 0]

sym_2 = y + x
=>
a = [0, 1, 0, 0, 1, 0]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 0, 0, 0, 1]



~out = sym_2 + 5
=>
a = [5, 0, 0, 0, 0, 1]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 1, 0, 0, 0]

'*' 对应系数分别在 a, b
'+' 对应系数都在a， b的常数系数为1

验证一下，x = 3 时，解向量 s = [1, 3, 35, 9, 27, 30]
第一行:

[1, 3, 35, 9, 27, 30] · [0, 1, 0, 0, 0, 0] * 
[1, 3, 35, 9, 27, 30] · [0, 1, 0, 0, 0, 0] - 
[1, 3, 35, 9, 27, 30] · [0, 0, 0, 1, 0, 0]
= 3 * 3 - 9 = 0

第二行

[1, 3, 35, 9, 27, 30] · [0, 0, 0, 1, 0, 0] * 
[1, 3, 35, 9, 27, 30] · [0, 1, 0, 0, 0, 0] - 
[1, 3, 35, 9, 27, 30] · [0, 0, 0, 0, 1, 0]
= 9 * 3 - 27 = 0

第三行

[1, 3, 35, 9, 27, 30] · [0, 1, 0, 0, 1, 0] * 
[1, 3, 35, 9, 27, 30] · [1, 0, 0, 0, 0, 0] - 
[1, 3, 35, 9, 27, 30] · [0, 0, 0, 0, 0, 1]
= （3 + 27）* 1 - 27 = 0

第四行

[1, 3, 35, 9, 27, 30] · [5, 0, 0, 0, 0, 1] * 
[1, 3, 35, 9, 27, 30] · [1, 0, 0, 0, 0, 0] - 
[1, 3, 35, 9, 27, 30] · [0, 0, 1, 0, 0, 0]
= （5 + 30）* 1 - 35 = 0

完整的 R1CS

A
[0, 1, 0, 0, 0, 0]
[0, 0, 0, 1, 0, 0]
[0, 1, 0, 0, 1, 0]
[5, 0, 0, 0, 0, 1]
B
[0, 1, 0, 0, 0, 0]
[0, 1, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
C
[0, 0, 0, 1, 0, 0]
[0, 0, 0, 0, 1, 0]
[0, 0, 0, 0, 0, 1]
[0, 0, 1, 0, 0, 0]

R1CS -> QAP

R1CS 可以完成证明，但对于一个解向量，验证时，有几个门电路就需要验证多少次。将 R1CS 转为 QAP(Quadratic Arithmetic Programs)，将四组三个长度为6的多项式，转变为6组3个3阶多项式。用多项式去代替向量的点积运算

We go from four groups of three vectors of length six to six groups of three degree-3 polynomials, where evaluating the polynomials at each x coordinate represents one of the constraints.

对于R1CS中的向量，转变为经过n个点的多项式（n 等于向量个数 4）

A
[0, 1, 0, 0, 0, 0]
[0, 0, 0, 1, 0, 0]
[0, 1, 0, 0, 1, 0]
[5, 0, 0, 0, 0, 1]

取每一列构造坐标，行号为x，值为 y
A 的第一列 [0, 0, 0, 5]
构造坐标 (1,0),(2,0),(3,0)(4,5)，求一个经过这四个点的多项式

拉格朗日插值法
通过n个点 (x1,y1),(x2,y2),…,(xn,yn) 的n-1阶多项式为如下所示：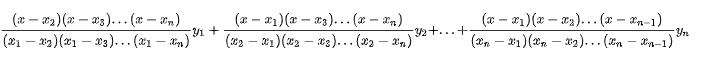

将(1,0),(2,0),(3,0)(4,5) 带入，求得多项式 0.833 x^3 - 5x^2 + 9.166x - 5

同理，计算出所有的多项式系数

A polynomials
[-5.0, 9.166, -5.0, 0.833]
[8.0, -11.333, 5.0, -0.666]
[0.0, 0.0, 0.0, 0.0]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]
[-1.0, 1.833, -1.0, 0.166]

B polynomials
[3.0, -5.166, 2.5, -0.333]
[-2.0, 5.166, -2.5, 0.333]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]

C polynomials
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[-1.0, 1.833, -1.0, 0.166]
[4.0, -4.333, 1.5, -0.166]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]

这样，x = 1 的时候，计算 18 个表达式，可以得到
[0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0]，正好对应 r1cs 的 A B C的第一行。

A
[0, 1, 0, 0, 0, 0]
[0, 0, 0, 1, 0, 0]
[0, 1, 0, 0, 1, 0]
[5, 0, 0, 0, 0, 1]
B
[0, 1, 0, 0, 0, 0]
[0, 1, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
C
[0, 0, 0, 1, 0, 0]
[0, 0, 0, 0, 1, 0]
[0, 0, 0, 0, 0, 1]
[0, 0, 1, 0, 0, 0]

记 A(x) = s · (A1,A2,A3,A4,A5,A6)

A(x) B(x) - C(x) = s·a s·b - s·c

同理， x = 1， 2， 3， 4 时，对应R1CS的4个约束， A(x) B(x) - C(x) = s·a s·b - s·c = 0
所以 A(x) B(x) - C(x) = 0 至少有 4 个解, 1, 2, 3, 4。
所以 A(x) B(x) - C(x) 可以表示为 (x - 1)(x - 2)(x - 3)(x - 4) H(x)
所以 A(x) B(x) - C(x) 如果能够整除 (x - 1)(x - 2)(x - 3)(x - 4)，就可以认为满足所有约束

验证：带入解向量 s = (1,3,35,9,27,30)，求得

A(x) = s · (A1,A2,A3,A4,A5,A6)
     = (1,3,35,9,27,30) ·（
[-5.0, 9.166, -5.0, 0.833]
[8.0, -11.333, 5.0, -0.666]
[0.0, 0.0, 0.0, 0.0]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]
[-1.0, 1.833, -1.0, 0.166]）
= [43.0, -73.333, 38.5, -5.166]  
（第一个系数43 = 1 * （-5） + 3 * 8 - 6 * 9 + 4 * 27 - 30）

同样

1 2	s . B = [-3.0, 10.333, -5.0, 0.666] s . C = [-41.0, 71.666, -24.5, 2.833]

// 顺序写反了？43应该是1的系数？
A(x) * B(x) - C(x) = 
(43 * x^3 - 73.333 * x^2 + 38.5 * x - 5.166) *
(-3 * x^3 + 10.333 * x^2 - 5 * x + 0.666) -
(-41 * x^3 - 71.666 * x^2 - 24.5 * x + 2.833) 
= -88 * x^6 + 592.666 * x^5 - 1063.777 * x^4 + 805 * x^3 
- 294.777 * x^2 + 51.5 * x -3.444


(x - 1)(x - 2)(x - 3)(x - 4)
= 24 * x^4 - 50 * x^3 + 35 * x^2 - 10 * x + 1

1 2	A(x) * B(x) - C(x) / (x - 1)(x - 2)(x - 3)(x - 4) = - 3.666 * x^2 - 17.055 * x - 3.444

能够整除，认为解 s 满足所有约束

相较于 R1CS，这部分用 R1CS 求出了多项式（系数）

A polynomials
[-5.0, 9.166, -5.0, 0.833]
[8.0, -11.333, 5.0, -0.666]
[0.0, 0.0, 0.0, 0.0]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]
[-1.0, 1.833, -1.0, 0.166]

B polynomials
[3.0, -5.166, 2.5, -0.333]
[-2.0, 5.166, -2.5, 0.333]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]

C polynomials
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[-1.0, 1.833, -1.0, 0.166]
[4.0, -4.333, 1.5, -0.166]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]

对于任意的解向量 s，计算 s · (A1,A2,A3,A4,A5,A6) × s · (B1,B2,B3,B4,B5,B6) - s · (C1,C2,C3,C4,C5,C6) 能否整除 (x - 1)(x - 2)(x - 3)(x - 4)

椭圆曲线

定义

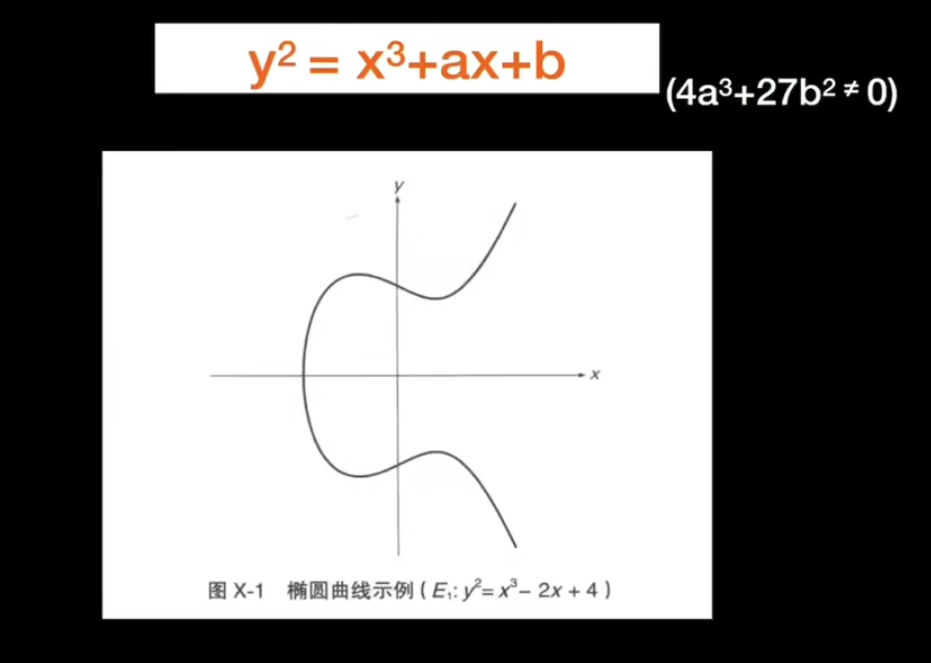
其中不等式保证曲线不包含奇点（保证椭圆上任意一点都有切线）
椭圆曲线关于 x 轴对称

椭圆曲线运算规则

加法：A + B

A B 是椭圆曲线上点，椭圆曲线上A + B的定义为：AB和椭圆曲线的交点关于X轴的对称点

乘法： 2A = A + A

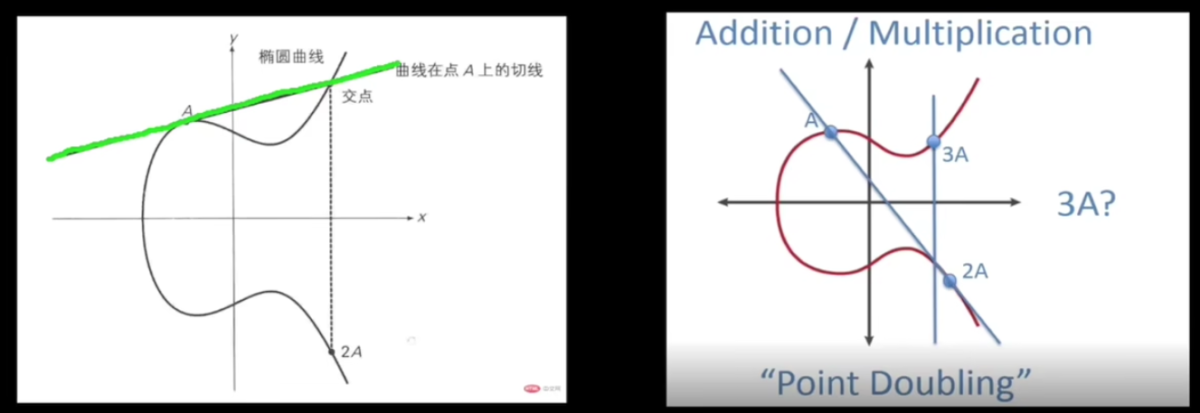
A 是椭圆曲线上点，椭圆曲线上 2A (A + A)的定义为：A点的切线和椭圆曲线的交点关于X轴的对称点
3A = A + 2A

性质

离散对数问题：
椭圆曲线上两个点 P Q， k为整数
Q = kP
加密原理：
点P为基点(base point), k 为私钥， Q 为公钥
给定 P 和 k，计算 Q 很容易，

但给定 P Q，求 k 非常困难

指数知识假设

在椭圆曲线上，给定一对点 (P,Q)，其中 Pk = Q ，然后在给定一个点 C ，你不可能得到一个点 R=Ck，除非你知道 C 是怎样由点 P “派生”出来的(比如你知道 C=nP 中的 n ，那么 Ck = nPk = nQ )。

1
2
3

Pk = Q  
C = nP 
Ck = R

zk-SNARK 的安全性依赖于这个假设，尽管其还没有被证明等价于其他困难问题（如离散对数问题），但是大多数密码学家认为它足够坚固。

zk - SNARK 证明

1
2
3

Pk = Q  
C = nP 
Ck = R

Pk = Q k = f(x) = 43 x^3 - 73.333 x^2 + 38.5 * x - 5.166 = k
给定PQ ，证明者无法算出 k

C = nP n = s
Ck = nPk = n Q = s Q = R
给定 CR，验已知k，可以验证 Ck = R
但根据 C = nP，无法计算 n，即解向量 s

椭圆曲线上任取一点 G, k_a，k_b，k_c， t

G * A_1(t), G * A_1(t) * k_a
G * A_2(t), G * A_2(t) * k_a
…
G * B_1(t), G * B_1(t) * k_b
G * B_2(t), G * B_2(t) * k_b
…
G * C_1(t), G * C_1(t) * k_c
G * C_2(t), G * C_2(t) * k_c
…

根据指数知识假设，只有知道解向量 s，才能够求出

π_a = G * A_1(t) * s, π_a' = G * A_1(t) * k_a * s
G * A_2(t) * s, G * A_2(t) * k_a * s
…
G * B_1(t) * s, G * B_1(t) * k_b * s
G * B_2(t) * s, G * B_2(t) * k_b * s
…
G * C_1(t) * s, G * C_1(t) * k_c * s
G * C_2(t) * s, G * C_2(t) * k_c * s

Ref

Quadratic Arithmetic Programs: from Zero to Hero： https://medium.com/@VitalikButerin/quadratic-arithmetic-programs-from-zero-to-hero-f6d558cea649?ref=blog.anoma.net
ETH ZKP： https://ethereum.org/zh/zero-knowledge-proofs/
VampIR：https://blog.anoma.net/a-vamp-irs-guide-to-arithmetic-circuits-and-perfectly-boiled-eggs/
【ECC加密算法】| ECC加密原理详解| 椭圆曲线加密| 密码学| 信息安全： https://www.bilibili.com/video/BV1v44y1b7Fd/?spm_id_from=333.337.search-card.all.click&vd_source=3f6c0363de570541eace117866128565
公钥加密技术ECC椭圆曲线加密算法原理： https://www.bilibili.com/video/BV1BY411M74G/?spm_id_from=333.337.search-card.all.click&vd_source=3f6c0363de570541eace117866128565

Write the code, Change the world

zk-SNARK学习

定义