二维凸包 Andrew算法

题目描述

LeetCode: 587.安装栅栏

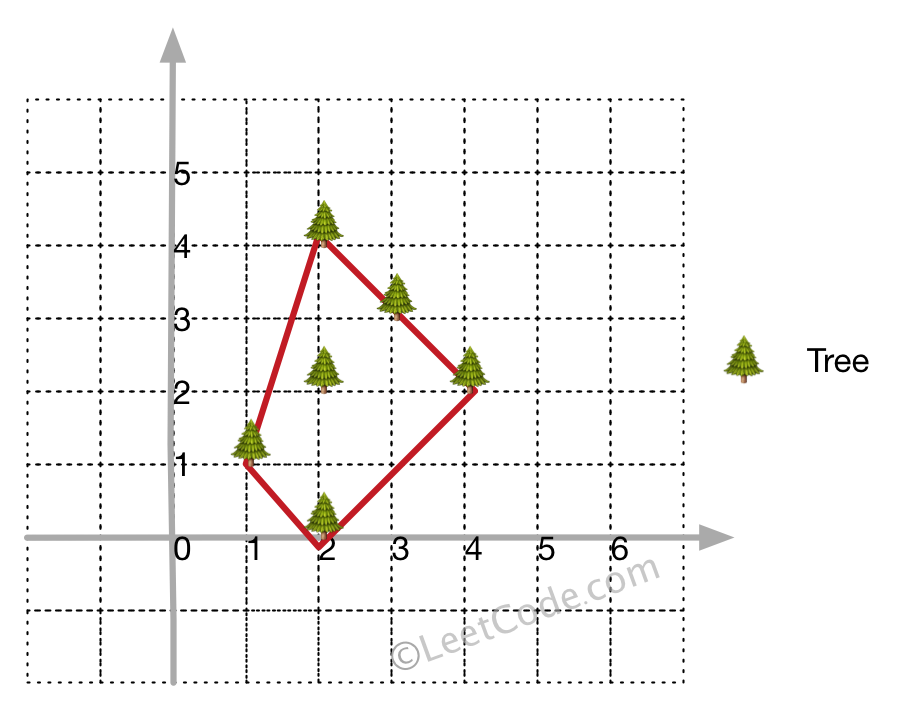
在一个二维的花园中，有一些用 (x, y) 坐标表示的树。由于安装费用十分昂贵，你的任务是先用最短的绳子围起所有的树。只有当所有的树都被绳子包围时，花园才能围好栅栏。你需要找到正好位于栅栏边界上的树的坐标。

示例:

input: [[1,1],[2,2],[2,0],[2,4],[3,3],[4,2]]
output: [[1,1],[2,0],[4,2],[3,3],[2,4]]

Andrew算法

算法思想

Andrew算法用于解决二维凸包问题。即在二维平面上用最小的周长包围所有点。因为周长最小，边界一定是凸多边形。所以从一个点出发，逆时针方向，相邻两条边夹角一定小于等于180°（向量夹角）。若大于，则一定不是边界的点，可以通过这样的方式来判断点是否在边界上。

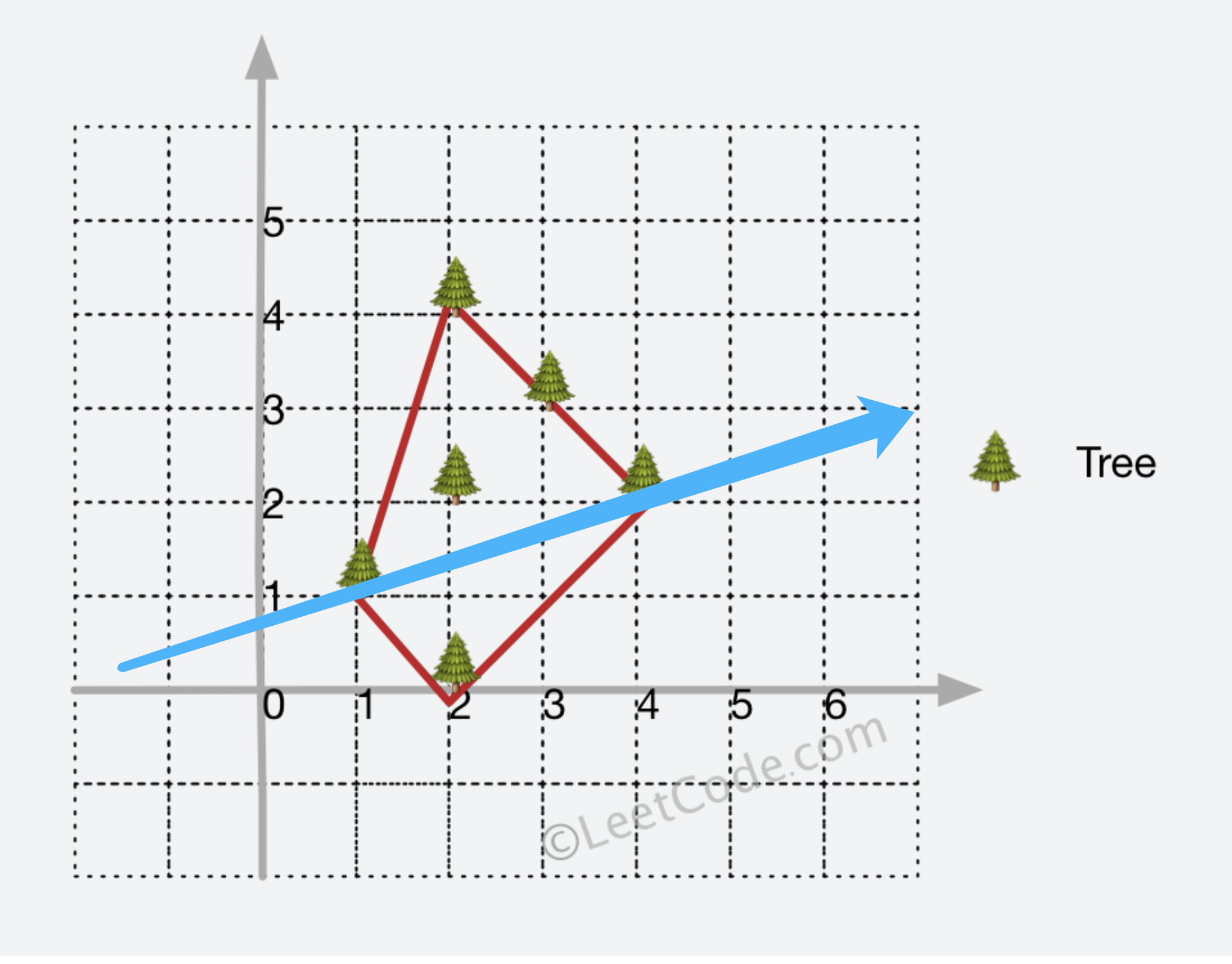
Andrew算法将凸包分为两部分，以边界最左和最右的两个节点的连线为分界线，分为上壳和下壳两部分。下壳从x坐标最小值顺时针“拐”到x最大值；上壳从最大值拐到最小值。

算法步骤

1. 根据x坐标升序排序，x相同则y升序排序
2. 用栈维护凸包（边界）上的点。
3. 计算下壳：从左到右遍历节点，对每一个新节点，与栈中最后一个节点组成一条边，栈中最后两个节点组成一条边，判断新节点是否在凸包上
4. 如果在凸包上，入栈，进入下一个节点
5. 如果不在凸包上，循环出栈，直至新节点与栈中最后一个节点组成的边在凸包上。
6. 如果栈中少于两个点，则节点直接入栈
7. 同理，从右到左遍历，计算上壳。

是否在凸包上的判断

用两个边的夹角（向量极角）来判断轨迹顺/逆时针旋转，即是否在凸包上。对于向量$\vec{pq}$,$\vec{qr}$,向量的叉积cross(p,q,r) =$\vec{pq}$×$\vec{qr}$，如果叉积小于 0，可以知道向量 $\vec{pq}$,$\vec{qr}$顺时针旋转，则此时向右拐；如果叉积大于 0，可以知道向量 $\vec{pq}$,$\vec{qr}$ 逆时针旋转，表示是左拐；如果叉积等于 0，则 $\vec{pq}$,$\vec{qr}$在同一条直线上。

def cross(p: List[int], q: List[int], r: List[int]) -> int:
    return (q[0] - p[0]) * (r[1] - q[1]) - (q[1] - p[1]) * (r[0] - q[0])

代码实现

class Solution:
    def outerTrees(self, trees: List[List[int]]) -> List[List[int]]:
        def cross(p: List[int], q: List[int], r: List[int]) -> int:
            return (q[0] - p[0]) * (r[1] - q[1]) - (q[1] - p[1]) * (r[0] - q[0])

        n = len(trees)
        if n < 4:
            return trees

        # 按照 x 从小到大排序，如果 x 相同，则按照 y 从小到大排序
        trees.sort()

        hull = [0]  # hull[0] 需要入栈两次，不标记
        used = [False] * n
        # 求凸包的下半部分
        for i in range(1, n):
            while len(hull) > 1 and cross(trees[hull[-2]], trees[hull[-1]], trees[i]) < 0:
                used[hull.pop()] = False
            used[i] = True
            hull.append(i)
        # 求凸包的上半部分
        m = len(hull)
        for i in range(n - 2, -1, -1):
            if not used[i]:
                while len(hull) > m and cross(trees[hull[-2]], trees[hull[-1]], trees[i]) < 0:
                    used[hull.pop()] = False
                used[i] = True
                hull.append(i)
        # hull[0] 同时参与凸包的上半部分检测，因此需去掉重复的 hull[0]
        hull.pop()

        return [trees[i] for i in hull]