合约审计与形式化验证: Certik 与 Move Prover
CertiK (https://www.certik.com/) 是 Web3 领先的智能合约审计公司,提供一整套工具来大规模保护行业安全。Certik 通过专家审查 + AI + 形式化验证保障合约安全。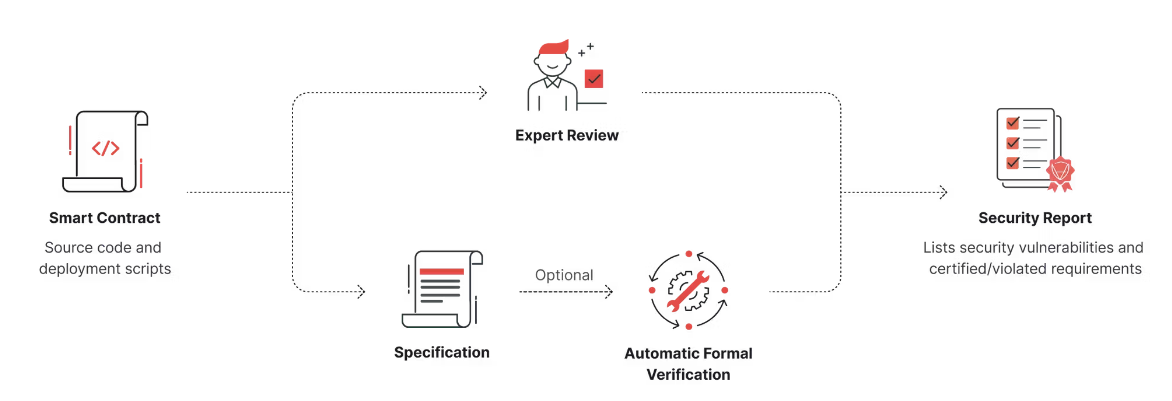
Certik 对智能合约的形式化验证主要过程为:
- 将合同的规范和所需属性定义为形式化语言。
- 将合约代码翻译成形式化表示,例如数学模型或逻辑。
- 使用自动定理证明器或模型检查器来验证合约的规范和属性是否成立。
- 重复验证过程以查找并修复与所需属性的任何错误或偏差。
Certik 使用 SMT Solver 和 Coq 作为形式化验证的工具。
- SMT: Formal Verification of ERC-20 Tokens
- Coq:
Certik 在更多的案例中使用了 Coq。Coq 是一个交互式的形式化验证工具。 它提供了一种用于编写数学定义、可执行算法和定理的形式语言,以及用于机器检查证明的半交互式开发的环境。
Move 是一种用于编写智能合约的特定领域编程语言。 它被几个最近启动的项目使用,包括 Aptos、0L 和 Starcoin 区块链。 Move 开发环境包括一个名为“Move Prover”的检查器。
Move 编程语言有一个规范子语言,允许程序员声明有关 Move 程序的所需属性。特别是,Move Prover 遵循合约范式设计。 在内部,Move Prover 将 Move 程序及其规范转换为数学模型,然后使用演绎验证器 Boogie 对其进行形式化验证。 Boogie 使用 Z3 和 CVC4 等 SMT 求解器作为决策程序来进行证明。 一旦 Boogie 完成形式验证,其结果就会映射回 Move 语言级别并显示给程序员。
SMT(satisfiability modulo theories) 求解器是 找到一组约束的可满足解: x - y = 3 x + y = 5 => x = 4 y = 1
合约/软件验证: 源代码 -> 建模 -> 约束 -> 对约束的反例求解 -> 有解则不满足约束,无解则满足约束
约束 x = y, 验证时: 对于 x != y,求解。所以 SMT 验证时的结果是给出一个反例和对应不满足的约束
Coq 和 Move Prover 的区别
用一个简单的例子感受 Coq 和 Move Prover之间的区别。
写一个 ERC20 中 transfer 函数,其实现与表示代币从一个合约地址转移到另一个地址。
1 | uint sender; |
这个合约实际上要求 sender >= amount,但在这个代码中并没有检查。接下来使用 Coq 和 Move Prover 来检查这一“漏洞”。
Coq
形式验证需要证明程序的模型满足所声明的属性。在这个例子中,可以选择代币总数作为不变量,验证“交易前后代币不变这一属性”。即交易前的 sender, receiver 和交易后的sender’, receiver’ 满足 sender + receiver = sender’ + receiver’
Certik 在使用 Coq 进行合约审计时,会将合约的实现翻译为 Coq 函数。我们将这个函数翻译为 Coq 中的一个 Definition。
1 | Definition transfer (sender receiver amount : nat) : nat := |
Coq是函数式编程语言,无副作用。不能直接更改输入的 sender receiver 的值。可以选择将交易后的 sender’ receiver’ 作为返回值,这里选择直接返回 sender’ + receiver’
然后,将模型需要满足的属性翻译为 Coq 中的引理。1
2Lemma transfer_eq : forall (a b c : nat),
a + b = transfer a b c.
这表示对于任意的自然数 a b c, a + b = transfer(a, b, c)
在开始证明之前,还需要引入一些Coq的标准库来辅助证明1
Require Import Arith.
使用 Proof. 来开始证明1
2
3
4
5
6
7
8Proof.
intros a b c.
unfold transfer.
rewrite (Nat.add_comm b c).
rewrite Nat.add_assoc.
rewrite Nat.sub_add.
reflexivity.
Abort.
Coq 是一个交互式的定理证明工具。在执行每一个证明语句后,证明的目标会发生改变。通过将证明的目标拆解为子目标,然后利用现有条件或公理、性质和已证明的引理来逐个证明。
一开始,证明的目标为:
使用 intros 引入 a b c 作为已知条件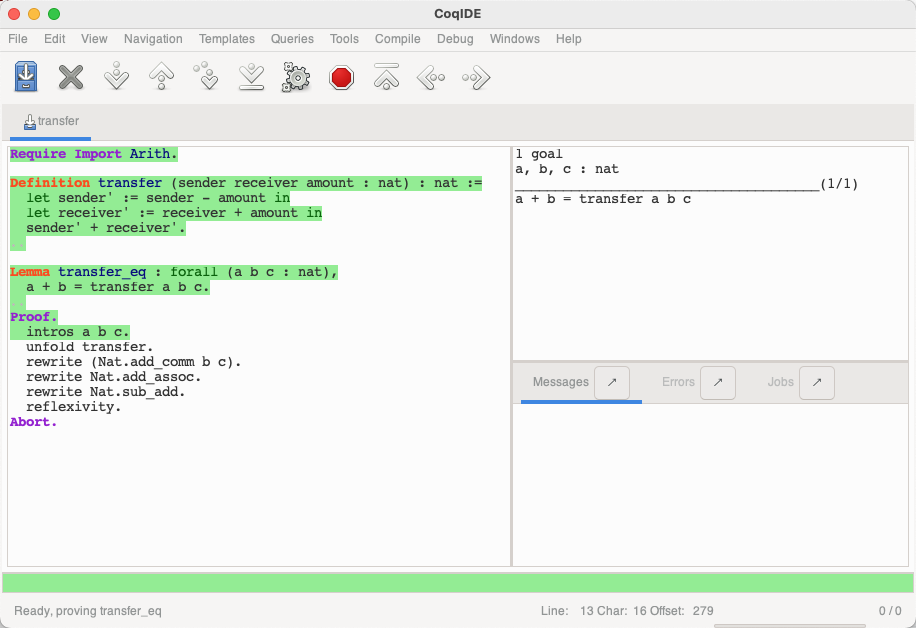
展开 transfer 函数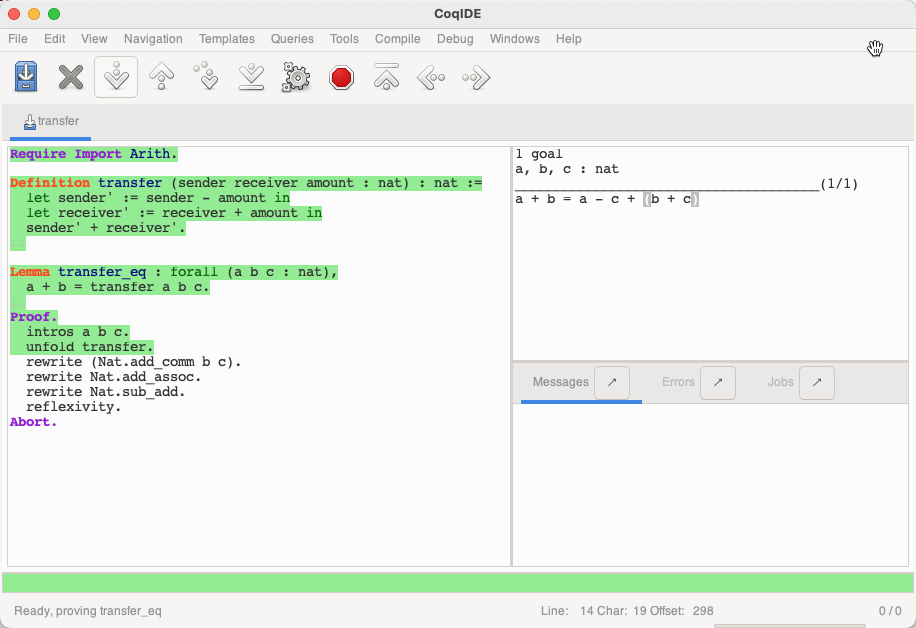
接下来使用标准库中的 Nat.add_comm Nat.add_assoc Nat.sub_add 来重写目标中的表达式
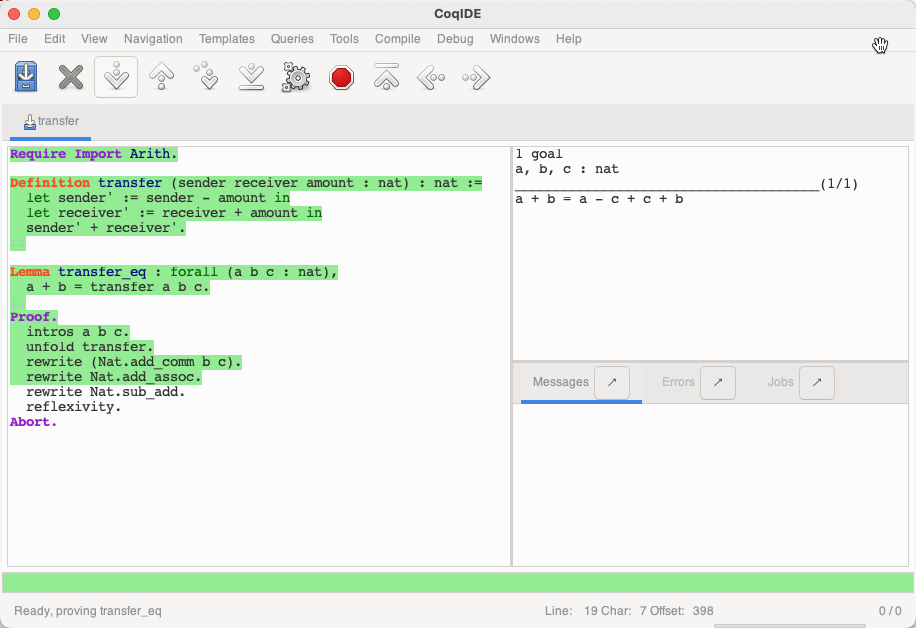
对于 Nat.sub_add, 查看其定义: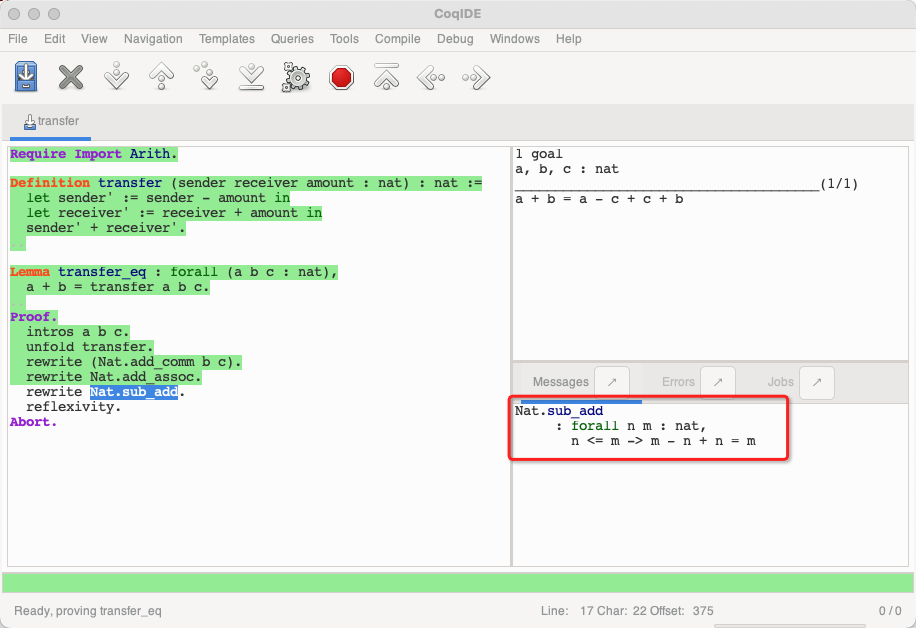
表示对于任意的自然数 n m, n <= m 时, m - n + n = m
对应此时目标中等号右边的 a - c + c。使用 Nat.sub_add 重写,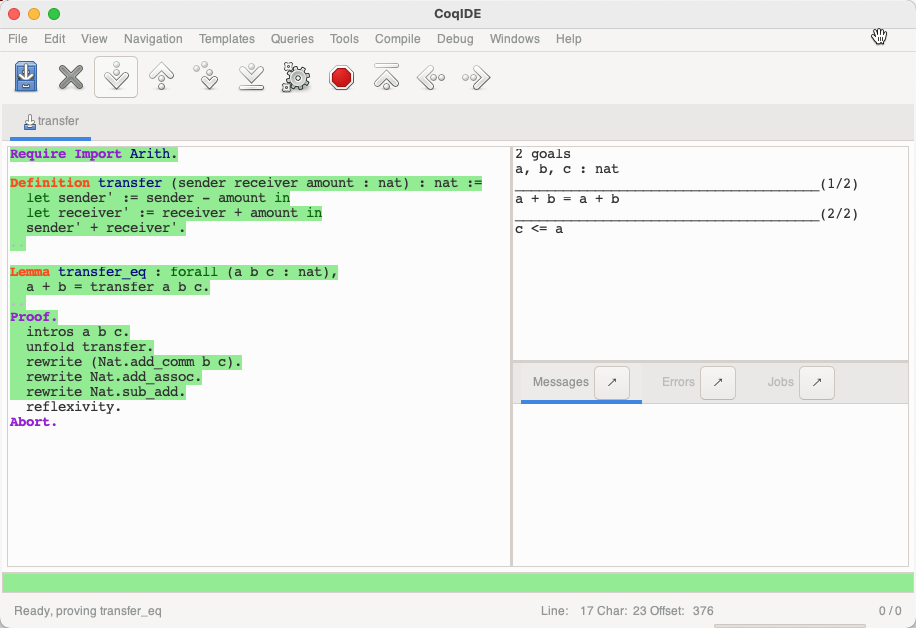
这里引入了新的目标,即 c <= a。是因为使用 Nat.sub_add 重写的前提为 c <= a。即将证明的目标反推,如果证明了 c <= a,并且 a + b = a + b,那么利用 Nat.sub_add 这一引理,就可以证明 a + b = a - c + c + b。
利用自反性(reflexivity)可以证明第一个目标。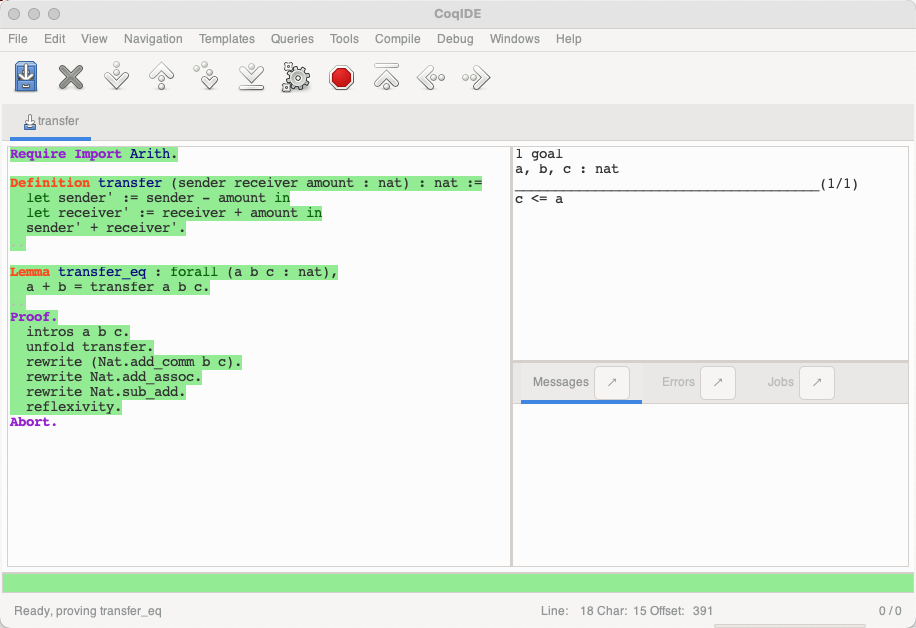
此时对于 c <= a 无从下手,只能 Abort 放弃证明,合约模型不满足这一属性。
此时回顾 c 和 a 在合约中的定义,分别表示amount 和 sender 的金额,这一条件要求 amount <= sender,很容易发现合约“漏洞”。
完整代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19Require Import Arith.
Definition transfer (sender receiver amount : nat) : nat :=
let sender' := sender - amount in
let receiver' := receiver + amount in
sender' + receiver'.
Lemma transfer_eq : forall (a b c : nat),
a + b = transfer a b c.
Proof.
intros a b c.
unfold transfer.
rewrite (Nat.add_comm b c).
rewrite Nat.add_assoc.
rewrite Nat.sub_add.
reflexivity.
Abort.
在线体验: https://coq.vercel.app/scratchpad.html
Move prover
1 | module 0x1234::test { |
运行 move prove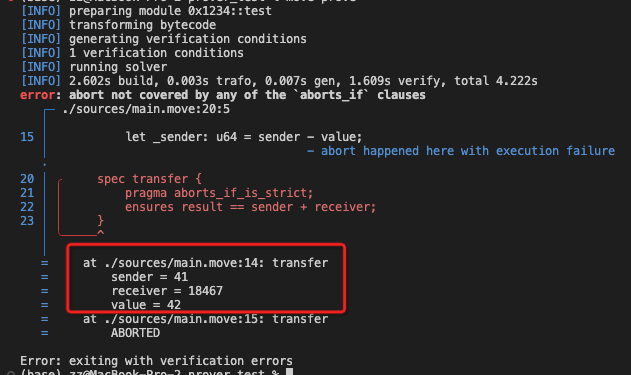
验证过程中,还会在当前项目目录下生成 boogie ir 的文件 xxx.bpl1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114// fun test::transfer [verification] at ./sources/main.move:2:5+183
procedure {:timeLimit 40} $1234_test_transfer$verify(_$t0: int, _$t1: int, _$t2: int) returns ($ret0: int)
{
// declare local variables
var $t3: int;
var $t4: int;
var $t5: int;
var $t6: int;
var $t7: int;
var $t8: int;
var $t0: int;
var $t1: int;
var $t2: int;
var $temp_0'u64': int;
$t0 := _$t0;
$t1 := _$t1;
$t2 := _$t2;
// verification entrypoint assumptions
call $InitVerification();
// bytecode translation starts here
// assume WellFormed($t0) at ./sources/main.move:2:5+1
assume {:print "$at(2,26,27)"} true;
assume $IsValid'u64'($t0);
// assume WellFormed($t1) at ./sources/main.move:2:5+1
assume $IsValid'u64'($t1);
// assume WellFormed($t2) at ./sources/main.move:2:5+1
assume $IsValid'u64'($t2);
// trace_local[sender]($t0) at ./sources/main.move:2:5+1
assume {:print "$track_local(0,0,0):", $t0} $t0 == $t0;
// trace_local[receiver]($t1) at ./sources/main.move:2:5+1
assume {:print "$track_local(0,0,1):", $t1} $t1 == $t1;
// trace_local[value]($t2) at ./sources/main.move:2:5+1
assume {:print "$track_local(0,0,2):", $t2} $t2 == $t2;
// $t5 := -($t0, $t2) on_abort goto L2 with $t6 at ./sources/main.move:3:35+1
assume {:print "$at(2,120,121)"} true;
call $t5 := $Sub($t0, $t2);
if ($abort_flag) {
assume {:print "$at(2,120,121)"} true;
$t6 := $abort_code;
assume {:print "$track_abort(0,0):", $t6} $t6 == $t6;
goto L2;
}
// trace_local[_sender]($t5) at ./sources/main.move:3:13+7
assume {:print "$track_local(0,0,4):", $t5} $t5 == $t5;
// $t7 := +($t1, $t2) on_abort goto L2 with $t6 at ./sources/main.move:4:39+1
assume {:print "$at(2,167,168)"} true;
call $t7 := $AddU64($t1, $t2);
if ($abort_flag) {
assume {:print "$at(2,167,168)"} true;
$t6 := $abort_code;
assume {:print "$track_abort(0,0):", $t6} $t6 == $t6;
goto L2;
}
// trace_local[_receiver]($t7) at ./sources/main.move:4:13+9
assume {:print "$track_local(0,0,3):", $t7} $t7 == $t7;
// $t8 := +($t5, $t7) on_abort goto L2 with $t6 at ./sources/main.move:5:17+1
assume {:print "$at(2,192,193)"} true;
call $t8 := $AddU64($t5, $t7);
if ($abort_flag) {
assume {:print "$at(2,192,193)"} true;
$t6 := $abort_code;
assume {:print "$track_abort(0,0):", $t6} $t6 == $t6;
goto L2;
}
// trace_return[0]($t8) at ./sources/main.move:5:9+19
assume {:print "$track_return(0,0,0):", $t8} $t8 == $t8;
// label L1 at ./sources/main.move:6:5+1
assume {:print "$at(2,208,209)"} true;
L1:
// assert Not(false) at ./sources/main.move:6:5+1
assume {:print "$at(2,208,209)"} true;
assert {:msg "assert_failed(2,208,209): function does not abort under this condition"}
!false;
// assert Eq<u64>($t8, Add($t0, $t1)) at ./sources/main.move:10:9+36
assume {:print "$at(2,275,311)"} true;
assert {:msg "assert_failed(2,275,311): post-condition does not hold"}
$IsEqual'u64'($t8, ($t0 + $t1));
// return $t8 at ./sources/main.move:10:9+36
$ret0 := $t8;
return;
// label L2 at ./sources/main.move:6:5+1
assume {:print "$at(2,208,209)"} true;
L2:
// assert false at ./sources/main.move:8:5+102
assume {:print "$at(2,215,317)"} true;
assert {:msg "assert_failed(2,215,317): abort not covered by any of the `aborts_if` clauses"}
false;
// abort($t6) at ./sources/main.move:8:5+102
$abort_code := $t6;
$abort_flag := true;
return;
}
- print: 打印调试信息,不影响执行
- $at 是一个 Boogie 的内置函数,用于指示某个语句或表达式的位置信息
- L1 L2, label,程序执行流程控制
- assume: 做一些前提假设。例如,assume WellFormed($t0) 表示假设 $t0 是一个合法的 Move 类型,并且 assume $IsValid’u64’($t0) 表示假设 $t0 是一个有效的无符号 64 位整数。这些假设在验证过程中用于推导其他断言。
- $abort_flag: 表示是否发生了异常(abort)
- assert: 断言,它用于在程序执行期间检查某个条件是否满足。如果断言条件为真,则程序继续执行;如果断言条件为假,则会导致验证失败。 例如 assert {:msg “assert_failed(2,275,311): post-condition does not hold”}
对比
Coq
优点:
- 从数学上证明,避免测试的 corner case
- 形式化的规范避免自然语言中的模糊和歧义
- 相对于 SMT,定理证明可以处理对无限状态系统的分析。上述例子中具体表现入参的区别, Coq 中可以对自然数域(nat 类型)做验证,而smt只能对有限的输入做验证
缺点
- 需要手动 translate,将智能合约的实现翻译为 Coq 代码,翻译的过程中可能导致 Coq 代码和原合约代码语义上的区别,例如 transfer 中 uint 变量类型被翻译为 nat
- 需要证明的合约满足的属性是不明确的。错误的约束可能会将漏洞从代码带到规范中,而不恰当的约束也可能导致错误不能被检查。这一点不只是coq,move prover 同样需要人为定义spec
- Coq需要手动证明,成本高,需要验证人员对 Coq 和智能合约都有认知。同时 Coq 证明也很复杂, Certik 在验证 TEE 时用了数千行的规范和 17300 多行的证明代码
- 过于 Customize,可以作为 Case by Case 的服务,但不太好沉淀为通用的解决方案。
Move prover
优点
- SMT 是自动求解的,不需要像Coq一样手动构造证明
- 更通用,完成语言前端到 boogie IR 的翻译之后,基本上所有语言都可以使用这个方案
缺点
- 语言设计时需要遵循SMT的约束,因此Move语言的能力有很大的限制,仅基础类型就不支持 int(只有 u8 u32 u64), string, map
- spec 很难写: https://github.com/move-language/move/blob/main/language/move-prover/doc/user/spec-lang.md
- SMT 存在状态爆炸和可判定问题https://en.wikipedia.org/wiki/Decision_problem
补充
符号执行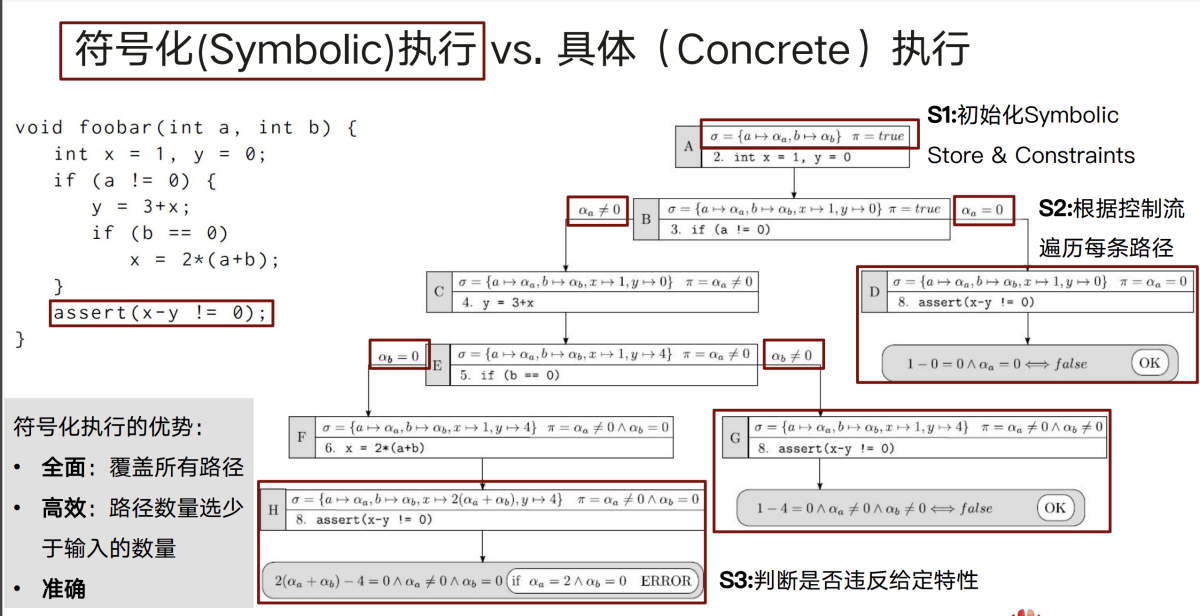
合约语言验证技术对比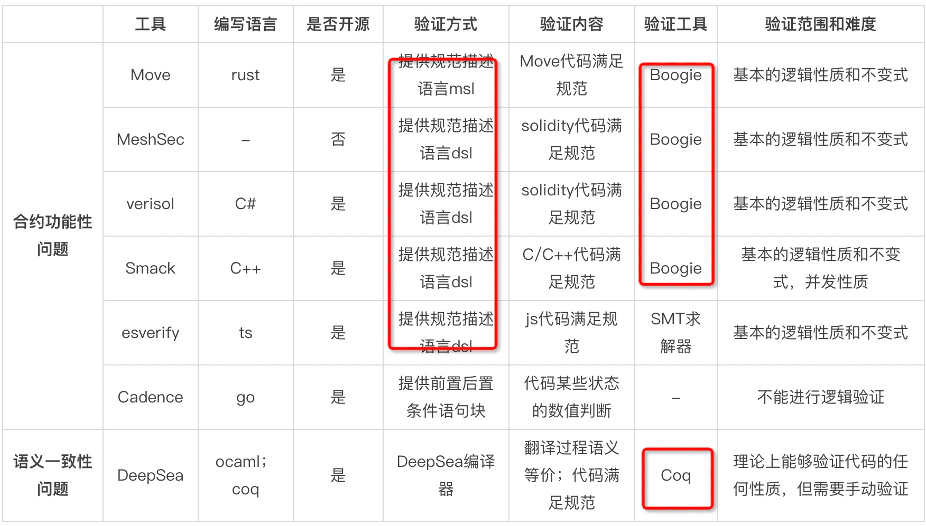
Solana Certora Prover 和 solidity SMTCheck 也是基于 SMT 的方案。
DeepSea 能采用 Coq 作为验证工具,大概率是因为语言使用 Ocaml 实现,Coq 由 Ocaml 语言实现且 Coq 代码可以提取为 Ocaml 代码,两者之间存在一些可转换性。
Todo
Solana Certora Prover (SCP)
- https://medium.com/certora/formal-verification-of-solana-smart-contracts-2e57b960f953
- https://medium.com/certora/formal-verification-of-spl-token-2022-d521db465c2e
Solidity SMTCheck
- https://docs.soliditylang.org/en/v0.8.15/smtchecker.html
- https://runtimeverification.com/blog/how-formal-verification-of-smart-contracts-works
Ref:
- https://ethereum.org/zh/developers/docs/smart-contracts/formal-verification/
- Advanced Web3 Formal Verification of HyperEnclave’s TEE
- Formal Verification of TON Master Chain Contracts
- How to Formally Verify A Cosmos SDK Standard Module
- Formal Verification of ERC-20 Tokens
- What is Formal Verification in Smart Contract Auditing? https://www.certik.com/resources/blog/3UDUMVAMia8ZibM7EmPf9f-what-is-formal-verification
- An Introduction to Move https://www.certik.com/resources/blog/3o4Cg1cjQH4IwA88aT8OwT-an-introduction-to-move
- Formal Verification, the Move Language, and the Move Prover https://www.certik.com/resources/blog/2wSOZ3mC55AB6CYol6Q2rP-formal-verification-the-move-language-and-the-move-prover
- https://github.com/move-language/move
- https://github.com/Zellic/move-prover-examples
- https://github.com/leonardoalt/ethereum_formal_verification_overview
- https://research.facebook.com/file/168513165302305/The-Move-Prover.pdf